曲線のまとめ

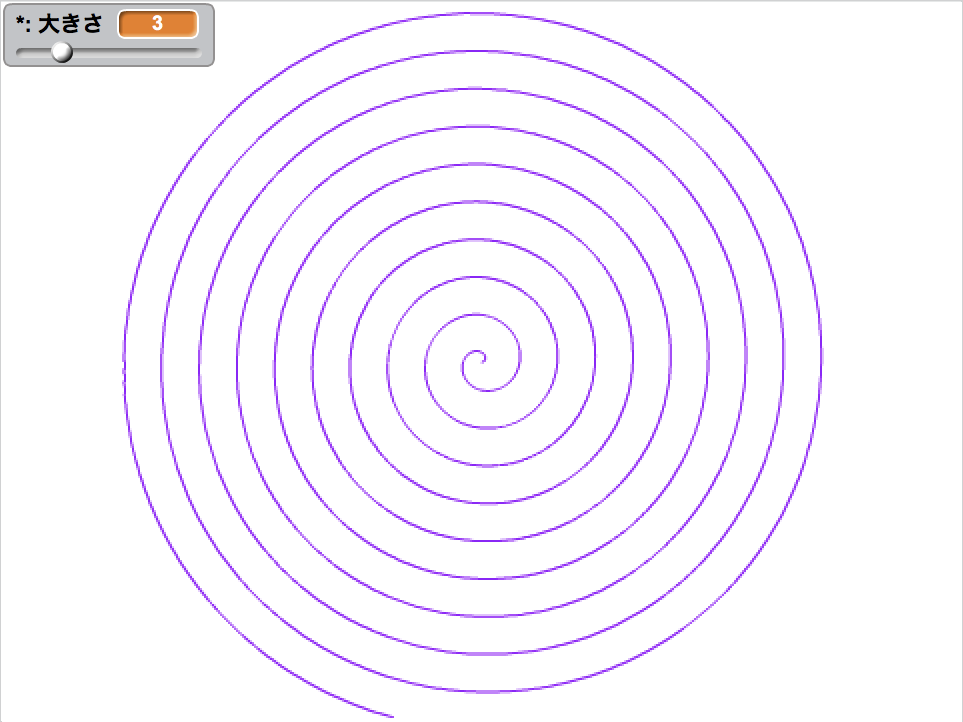
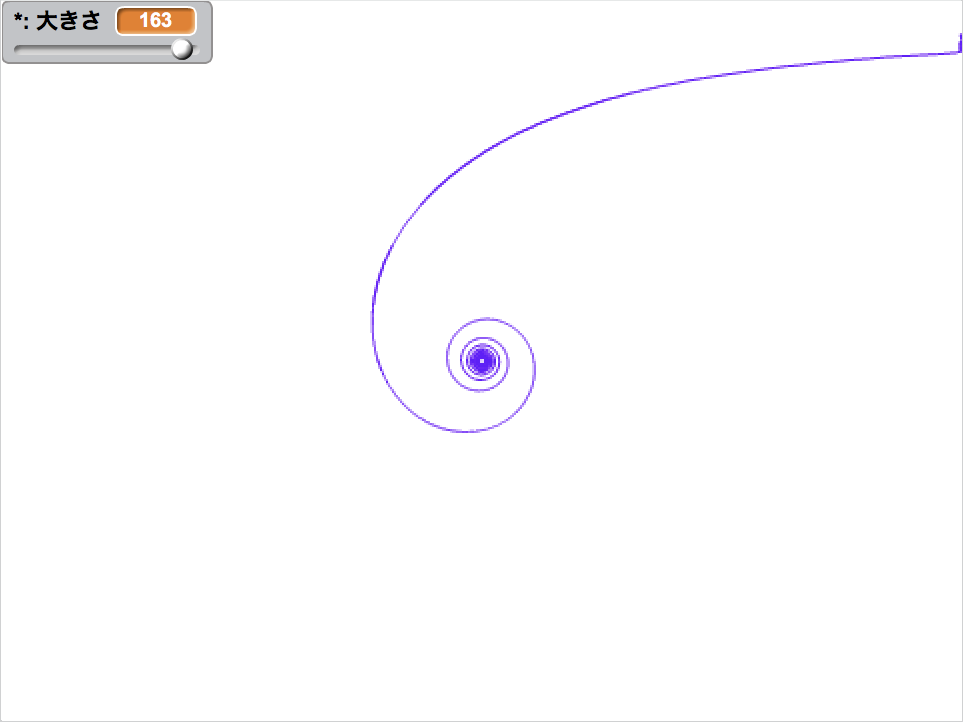
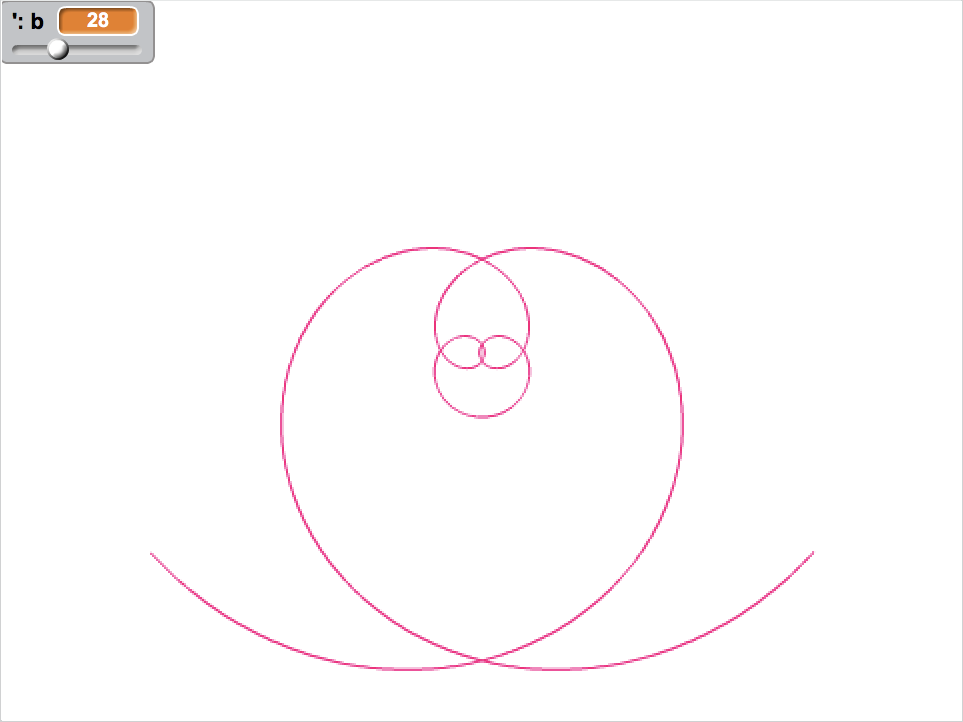
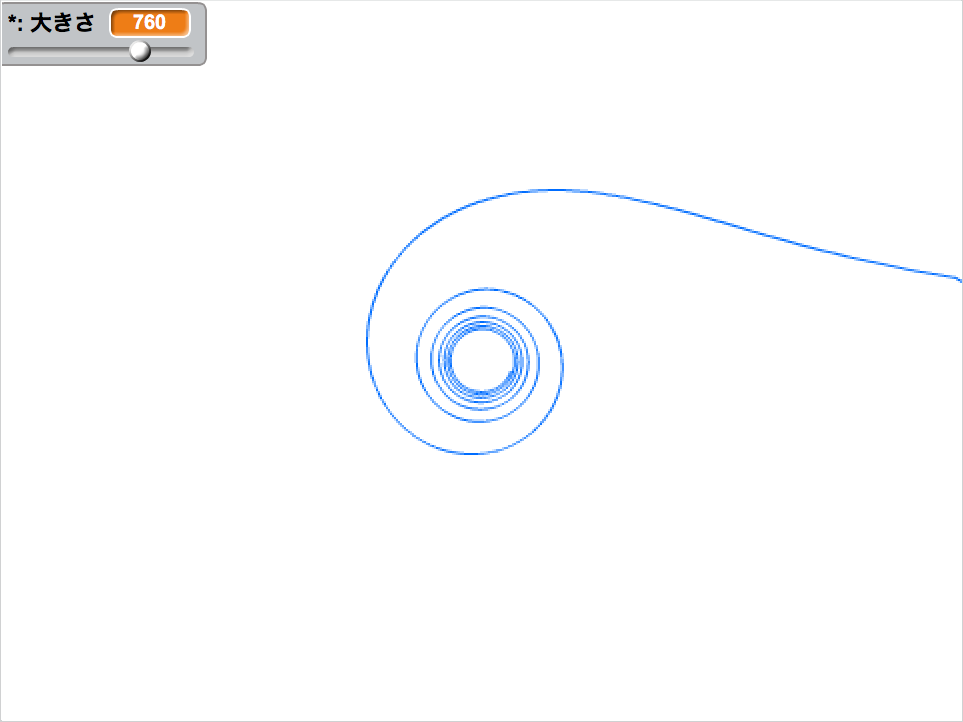
これまでに紹介した曲線を一覧にしました。厳密ではないですが、単純な式から順に並べています。

名称、式、Scratch列のセルはリンクになっています。

ブラウザによっては画像が全部表示されないかもしれません。そのような場合は、その画像だけ再読み込みしてください。

極座標方程式

名称	式	曲線	Scratch
アルキメデスのらせん	\[ r=a\theta \]
双曲らせん	\[ r=\frac{a}{\theta} \]
Neoid	\[ r=a\theta+b \]
ガリレオのらせん	\[ r=a+b\theta^2 \]
放物らせん	\[ r=a\sqrt{\theta} \]
フェルマーのらせん	\[ r=\pm a\sqrt{\theta} \]
リチュース	\[ r=\frac{a}{\sqrt{\theta}} \]
対数らせん	\[ r=ae^{b\theta} \]
カタランの曲線	\[ r=\frac{a}{1-\theta^2}\]
三つ葉	\[ r=a\cos(3\theta) \]
四つ葉	\[ r=a\sin(2\theta) \]
バラ曲線	\[ r=\sin\left(\frac{n}{d}\theta\right) \]
デューラーの葉形曲線	\[ r=a\sin\left(\frac{\theta}{2}\right) \]
ガーフィールド曲線	\[ r=\theta\cos(\theta) \]
Double Egg	\[ r=a\cos^2(\theta) \]
ケプラーの卵	\[ r=a\cos^3(\theta) \]
チェバのサイクロイド	\[ r=1+2\cos(2\theta) \]
カージオイド	\[ r=a(1+\cos(\theta)) \]
Cyclic-Harmonic Curve	\[ r=a\left(1+e\cos(n\theta)\right) \]
パスカルの蝸牛形	\[ r=a(1+2\cos(\theta)) \]
スカラベ曲線	\[ r=a\cos(2\theta)-b\cos(\theta) \]
二つ葉	\[ r=a\left(\sin(\theta)+\sin(3\theta)\right) \]
魚雷曲線	\[ r=a\cos(\theta)\cos(2\theta) \]
コクレオイド	\[ r=\frac{a\sin(\theta)}{\theta} \]
Equilateral Trefoil	\[ r=\frac{a}{\cos(3\theta)} \]
チェバの五等分曲線	\[ r=a\frac{\sin(5\theta)}{\sin(\theta)} \]
5次曲線	\[ r=\frac{a\sin(\theta)}{1+\cos(\theta)\cos(2\theta)} \]
四つ葉 (2)	\[ r=a\left(\sin^2(2\theta)+\frac{\sin^2(4\theta)}{2}\right) \]
マクローリンの三等分曲線	\[ r=a\left(4\cos(\theta)-\frac{1}{\cos(\theta)}\right) \]
頭蓋曲線 (Cranioid)	\[ r=a\sin(\theta)+b\sqrt{1-p\cos^2(\theta)}+c\sqrt{1-q\cos^2(\theta)} \]
カッシーニ曲線	\[ r=a\sqrt{cos(n\theta)\pm\sqrt{e^{2n}-sin^2(n\theta)}} \]
ひげぜんまい曲線	\[ r=\frac{a}{1+ke^{m\theta}} \]
バタフライ曲線	\[ r=e^{sin(\theta)}-2\cos(4\theta)-sin^5\left(\frac{2\theta-\pi}{24}\right) \]
ストロフォイド	\[ r=-\frac{a\cos(2\theta)}{\cos(\theta)} \]
デカルトの正葉線	\[ r=\frac{3a\sin(\theta)\cos(\theta)}{sin^3(\theta)+cos^3(\theta)} \]
Cayley's Sextic	\[ r=4a\cos^3\left(\frac{1}{3}\theta\right) \]
Freeth's Nephroid	\[ r=a\left(1+2\sin\left(\frac{1}{2}\theta\right)\right) \]
豆曲線	\[ r=\sin^3(\theta)+\cos^3(\theta) \]
Jerabek Curve	\[ r=a\frac{k\cos(\theta)-1}{k-\cos(\theta)} \]
三つ葉(2) (Kiepert Curve)	\[ r=a\sqrt[3]{cos(3\theta)} \]
Capricornoid	\[ r= a\frac{\sin(\theta)}{\cos(\theta)+b} \]
蝶結び曲線	\[ r=\frac{\sin(\theta)\times(1-2sin^2(\theta))}{cos^4(\theta)} \]
双曲正接らせん	\[ r=a\tanh(k\theta) \]
ポアンソーのらせん (双曲正割関数)	\[ \newcommand{\sech}{\mathop{\rm sech}\nolimits} r=a\sech(n\theta) \]
ポアンソーの螺旋 (双曲余割関数)	\[ \newcommand{\csch}{\mathop{\rm csch}\nolimits} r=a\csch(n\theta) \]
歯車	\[ r=a+\frac{1}{b}\tanh(b\sin(n\theta)) \]
Tschirnhausen Cubic	\[ r=a \sec^3\left(\frac{1}{3}\theta\right) \]
風車	\[ r=a\tan(2\theta) \]
風車2	\[ r^2=\lvert\cot(2\theta)\rvert \]
左まんじ	\[ r^2=\tan(2\theta) \]
Right Serpentine	\[ r^2=a^2\cot(\theta) \]
ダイポール曲線	\[ r^2=a^2\cos(\theta) \]
レムニスケート	\[ r^2=2a^2\cos(2\theta) \]
Hippopede	\[ r^2=4b(a-b\sin^2(\theta)) \]
ブースの楕円	\[ r^2=a^2\cos^2(\theta)+b^2\sin^2(\theta) \]
ブースのレムニスレート	\[ r^2=a^2\cos^2(\theta)-b^2\sin^2(\theta) \]
ワットの曲線	\[ r^2=b^2-\left(a\sin(\theta)\pm\sqrt{c^2-a^2\cos^2(\theta)}\right)^2 \]
カッシーニの卵形線	\[ r^2=a^2\left(\cos(2\theta)\pm\sqrt{\left(\frac{b}{a}\right)-sin^2(2\theta)}\right) \]

媒介変数方程式

名称	式	曲線	Scratch
サイクロイド	\[ x=r\left(\theta-\sin(\theta)\right) \\ y=r\left(1-\cos(\theta)\right)\]
洋梨曲線	\[ x = a\sin(\theta)\\ y=b\cos(\theta)(1+\sin(\theta)) \]
ハート	\[ x = 16\sin^3(\theta) \\ y = 13\cos(\theta)-5\cos(2\theta)-2\cos(3\theta)-\cos(4\theta) \]
キス曲線	\[ x = a\cos(\theta) \\ y = a\sin^5(\theta) \]
アステロイド曲線	\[ x=a\cos^b(\theta) \\ y=a\sin^b(\theta) \]
Cross Curve	\[ x=\frac{a}{\sin{\theta}} \\ y=\frac{b}{\cos(\theta)}\]
リサージュ	\[ x=A\cos(a\theta) \\ y=A\sin(b\theta) \]
インボリュート	\[ x=a\left(\cos(\theta)+\theta sin(\theta)\right) \\ y=a\left(\sin(\theta)-\theta cos(\theta)\right) \]
8曲線 Lemniscate of Gerono	\[ x=a\sin(\theta) \\ y=a\sin(\theta)cos(\theta) \]
ダンベル曲線(平方根版)	\[ x=a\theta \\ y=a\theta^2\sqrt{1-\theta^2} \]
ダンベル曲線(sin/cos版)	\[ x=a\cos(\theta) \\ y=a\cos^2(\theta)\sin(\theta)\]
魚曲線	\[ x=a\cos(\theta) - \frac{a\sin^2(\theta)}{\sqrt2} \\ y=a\cos(\theta)\sin(\theta) \]
Bicorn	\[ x= a\sin(\theta) \\ y= \frac{a\cos^2(\theta)(2+\cos(\theta))}{3+\sin^2(\theta)} \]
スピログラフ	\[ x=(R-r)\cos(\theta)+p\cos\left(\frac{R-r}{r}\theta\right) \\ y=(R-r)\sin(\theta)-p\sin\left(\frac{R-r}{r}\theta\right) \]
外サイクロイド	\[ x=(R+r)\cos(\theta)-r\cos\left(\frac{R+r}{r}\theta\right) \\ y=(R+r)\sin(\theta)-r\sin\left(\frac{R+r}{r}\theta\right) \]
内サイクロイド	\[ x=(R-r)\cos(\theta)+r\cos\left(\frac{R-r}{r}\theta\right) \\ y=(R-r)\sin(\theta)-r\sin\left(\frac{R-r}{r}\theta\right) \]
外トロコイド	\[ x=(R+r)\cos(\theta)-d\cos\left(\frac{R+r}{r}\theta\right) \\ y=(R+r)\sin(\theta)-d\sin\left(\frac{R+r}{r}\theta\right) \]
内トロコイド	\[ x=(R-r)\cos(\theta)+d\cos\left(\frac{R-r}{r}\theta\right) \\ y=(R-r)\sin(\theta)-d\sin\left(\frac{R-r}{r}\theta\right) \]
Squircle	\[ \newcommand{\sgn}{\mathop{\rm sgn}\nolimits} x=\sqrt{|\cos(\theta)|} \times r\sgn(\cos(\theta)) \\ y=\sqrt{|\sin(\theta)|} \times r\sgn(\sin(\theta))\] sgnは引数の符号を取り出す関数
ネフロイド Nephroid	\[ x= 6a\cos(\theta)-4a\cos^3(\theta) \\ y=4a\sin^3(\theta) \]
プラトーの曲線	\[ x=\frac{a\sin((m+n)\theta)}{\sin((m-n)\theta)} \\ y=\frac{2a\sin(m\theta)sin(n\theta)}{\sin((m-n)\theta)}\]
涙曲線	\[ x= \cos(\theta)\\ y=\sin(\theta)\sin^m\left(\frac{1}{2}\theta\right)\]
Besace	\[ x= a\cos(\theta)-b\sin(\theta) \\ y=-(\sin(\theta))x \]
Carlos Sacréの8次曲線	\[ x=\sin(3\theta)\cos(\theta) \\ y=(\sin(3\theta)\sin(\theta))^2 \]
Siamese fishes	\[ x=5\cos(\theta)-(\sqrt{2}-1)\cos(5\theta) \\ y=\sin(4\theta)\]
三芒形	\[ x=2a\cos(\theta)+a\cos(2\theta) \\ y=2a\sin(\theta)-a\sin(2\theta) \]
Quadratrix of Abdank-Abakanowicz	\[ x=R\sin(\theta) \\ y=\frac{R^2}{2}(\theta+\sin(\theta)\cos(\theta)) \]
Basin	\[ x=\sin(\theta)\cos(3\theta) \\ y=\cos^2(3\theta) \]
円と8	\[ x=2\sin(2\theta) \\ y=\cos(\theta)+\cos(3\theta) \]
マルタ十字	\[ x=a\cos(\theta)\left(\cos^2(\theta)-2\right) \\ y=a\sin(\theta)cos^2(\theta) \]
Cornoid	\[ x=a\cos(\theta)\left(1-2\sin^2(\theta)\right) \\ y=a\sin(\theta)\left(1+2\cos^2(\theta)\right) \]
Hügelschäffer Egg	\[ x= \left(\sqrt{a^2-d^2\sin^2(\theta)}+d\cos(\theta)\right)\cos(\theta) \\ y=b\sin(\theta) \]
円とカージオイド	\[ x= \frac{\cos^3(\theta)}{2\cos^3(\theta)-2\cos(\theta)+1} \\ y=\frac{\sin(2\theta)\sin^2\left(\frac{\theta}{2}\right)}{2\cos^3(\theta)-2\cos(\theta)+1} \]
Talbot Curve	\[ x=a\cos(\theta)\left(1+\frac{a^2-b^2}{a^2}\sin^2(\theta)\right) \\ y=b\sin(\theta)\left(1-\frac{a^2-b^2}{b^2}\cos^2(\theta)\right)\]
Septic	\[ x=\frac{\cos(\theta)(3\cos^2(\theta)-3\cos(\theta)+1)}{2\cos^3(\theta)-2\cos(\theta)+1} \\ y=\frac{\cos^2(\theta)\sin(\theta)}{2\cos^3(\theta)-2\cos(\theta)+1}\tan^2\left(\frac{\theta}{2}\right)\]
クロソイド	\[ x=\int_0^L \cos\left(t^2\right)dt \\y=\int_0^L \sin\left(t^2\right)dt \]

タグ：三角関数 SCRATCH 平面曲線

ギャラリー2

4月以降の曲線をまとめました。前回のギャラリーはこちら。

画像をクリックすると各記事に飛びます。

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

タグ：平面曲線 三角関数 SCRATCH

クロソイド

Scratchでクロソイドを描きます。Wolfram Mathworldやmathcurve.comで公開されている式をもとにした曲線はこれで一旦終了です。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

今回は、WikipediaにあるJavaScriptのソースコードを参考にプログラムを作りました。積分を使うのでいつもとは少し処理が違います。

最初に本体です。この曲線は右上部分と左下部分に分けて原点(0,0)から二回描画しますので、繰り返しが二回あります。



次に変数です。



次に準備です。右上の描画前と左下の描画前に一度ずつ呼び出されます。



式はこうなっています。tは角度です。
\[ x=\int_0^L \cos\left(t^2\right)dt \\y=\int_0^L \sin\left(t^2\right)dt \] この式をプログラムにすると次のようになります。式のインテグラル（積分）の繰り返し部分は本体に存在します。



ラジアンから角度を求めるブロックは次の通りです。



移動はいつも通りです。



完成版はこちら。

タグ：SCRATCH 三角関数 平面曲線

Tschirnhausen Cubic

ScratchでTschirnhausen Cubicを描きます。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

最初に変数です。secは関数の計算結果を保存しておくための変数です。そのほかはいつも通りです。



次に本体です。角度を-191度から191度まで変化させながら計算、移動を繰り返すとこの曲線が描画できます。



次に準備です。ペンの設定、変数の初期化、開始座標の計算、開始座標への移動を行なっています。



この曲線を描画するための式はこうなっています。rは半径、aは倍率(大きさ)、θは角度です。
\[ r=a \sec^3\left(\frac{1}{3}\theta\right) \] この式をプログラムにすると次のようになります。



secは正割関数です。定義はこうなっています。
\[sec(\theta)=\frac{1}{cos(\theta)} \] この式をプログラムにすると次のようになります。



このブロックの計算結果は変数「sec」に格納しておき、計算の中で使っています。

移動はいつも通りです。



完成版はこちら。

タグ：三角関数 SCRATCH

歯車 Gear Curve

Scratchで歯車を描きます。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

最初に変数です。今回は倍率は固定で、歯車の歯の数を可変にしています。tanhは関数の計算結果を保持しておくための変数です。また、bは式の中で出てくる定数で、準備処理の中で10に固定しています。



次に本体です。角度を0度から360度まで変化させながら計算、移動を繰り返すとこの曲線が描画できます。



次に準備です。ペンの設定、変数の初期化、開始座標の計算、開始座標への移動を行なっています。



式はこうなっています。rは半径、aは倍率(大きさ)、θは角度です。
\[ r=a+\frac{1}{b}\tanh(b\sin(n\theta)) \] tanhは双曲正接関数です。bを大きくすると歯の高さが小さくなります。今回は10に固定していますが、スライダ表示にして変化させてみるのも面白いですよ。

この式をプログラムにすると次のようになります。上の式の「a」は1に固定、いつも曲線の大きさの調整に使っている「倍率」変数は上の「準備」処理で160に固定しています。



tanhはWikipediaで次のように定義されています。eはネイピア数です。
\[ \tanh(\theta)=\frac{1-e^{-2\theta}}{1+e^{-2\theta}} \] これはScratchでは提供されていないので、自分でブロックを作って定義します。



計算結果はtanh変数に保存しておき、計算で使っています。

移動はいつも通りです。



完成版はこちら。

タグ：平面曲線 SCRATCH 歯車 三角関数

ポアンソーのらせん Poinsot's spiral (csch)

Scratchでポアンソーのらせん (csch版)を描きます。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

最初に変数です。cschとラジアンは関数の計算結果をあとで使うために保持しておく変数です。



次に本体です。最初に角度を60度から810度まで変化させながら計算、描画を繰り返します。次に角度の符号を反転させて-810度から-60度まで計算、描画を繰り返します。



-60度から60度の間を描画しないのは、曲線が画面の外側にはみ出したり符号が反転する時に余計な線が描画されたりするからです。

次に準備です。ペンの準備、変数の初期設定、開始座標の計算、開始座標への移動を行なっています。



式はこうなっています。rは半径、aは倍率(大きさ)、θは角度です。nも曲線の大きさに影響します。
\[ \newcommand{\csch}{\mathop{\rm csch}\nolimits} r=a\csch\left(n\theta\right) \] この式をプログラムにすると次のようになります。今回は \(n=\frac{1}{3}\) としています。最初にcsch関数の値を計算し、その結果から半径を計算、さらに半径と角度からX座標とY座標を計算しています。最後にY座標を下に移動して曲線全体が画面内に収まるように調整しています。



cschは双曲余割関数です。Scratchでは提供されていないので、Wolfram Mathworldの定義を使って自分でブロックを定義します。
\[ \csch(\theta)=\frac{2}{e^{\theta}-e^{-\theta}} \] \(e\) はネイピア数です。この式をプログラムにすると次のようになります。



計算結果はcsch変数に入れておき、計算の中で使います。

ラジアンもブロックを定義します。Scratchでは事前に定義されている三角関数には角度の値をそのまま使いますが、自分で定義する関数はラジアンを使う必要があります。



移動はいつも通りです。



完成版はこちら。

タグ：SCRATCH 三角関数 平面曲線

ポアンソーのらせん Poinsot's spiral (sech)

Scratchでポアンソーのらせん(sech版)を描きます。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

最初に変数です。sechは同名の関数の計算結果を保存しておくための変数です。大きさはスライダー表示にして画面上で値を変更できるようにしています。



次に本体です。角度を-1080度から1080度まで変化させながら計算、描画を繰り返すと、この曲線が描画できます。



次に準備です。ペンの設定、変数の初期設定、開始座標の計算、開始座標への移動を行なっています。



式はこうなっています。rは半径、aは倍率（大きさ）、θは角度です。nも曲線の大きさに影響します。
\[ \newcommand{\sech}{\mathop{\rm sech}\nolimits} r=a\sech\left(n\theta\right) \] 今回は \(n=\frac{1}{3}\) としています。この式をプログラムにすると次のようになります。まずsechを計算し、その結果から半径を計算、さらに半径と角度からX座標とY座標を計算しています。



sechは双曲正割関数です。Scratchにはこの関数は用意されていませんので、Wolfram Mathworldの定義を使って、自分でブロックを定義します。
\[ \sech(\theta)=\frac{2}{e^{\theta}+e^{-\theta}} \] \(e\) はネイピア数です。この式をプログラムにすると次のようになります。



Scratchでは内蔵されている三角関数には角度を指定しますが、自分で定義する関数の角度にはラジアンを使いますので、ラジアンのブロックも定義しています。



移動はいつも通りです。



完成版はこちら。

タグ：平面曲線 SCRATCH 三角関数

双曲正接らせん Hyperbolic Tangent Spiral

Scratchで双曲正接らせんを描きます。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

最初に変数です。tanhは三角関数の計算結果を保持するための変数です。「大きさ」と「k」はスライダー表示にして画面上で変更できるようにしています。



次に本体です。角度を-450度から450度まで変化させながら計算、移動を繰り返すとこの曲線を描画できます。



次に準備です。ペンの設定、変数の設定、開始座標の計算、開始座標への移動を行なっています。



式はこうなっています。rは半径、aは倍率(大きさ)、θは角度です。
\[ r=a\tanh(k\theta) \] この式をプログラムにすると次のようになります。



最初に\(\tanh(\theta)\)から半径を計算し、その結果からX座標とY座標を計算しています。\(\tanh\)は双曲正接関数で、今回はこのサイトにある定義を使っています。
\[ \tanh(\theta)=\frac{e^{\theta}-e^{-\theta}}{e^{\theta}+e^{-\theta}} \] \(e\) はネイピア数です。Scratchにはこの関数は備わっていないので、自分でブロックを定義します。



移動はいつも通りです。



完成版はこちら。

タグ：SCRATCH 平面曲線 三角関数

内トロコイド Hypotrocoid

Scratchで内トロコイドを描きます。式は前回の外トロコイドや前々回の内サイクロイド、その前の外サイクロイド、以前のスピログラフに似ています。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

最初に変数です。上のWikipediaのリンクを見るとわかりますが、内トロコイドは中心の定円の内側を動円が回転する軌跡になっています。このため、外側の円の「定円半径」と回転する円の「動円半径」、さらに動く円の中心から描画点までの「描画点半径」を変数として持っています。これら三種類の半径はスライダー表示にして画面上で値を変更できるようにしています。値を変えると曲線の形が変わります。



次に本体です。角度を0.5度ずつ変化させながら描画を続けます。繰り返しの終了条件がない理由は外トロコイドと同じで、スライダーで指定する各半径の値によって終了条件が変わるからです。描画を止めるには、旗の右にある赤いボタンを押してください。描画には時間がかかるのでターボモードがお勧めです。



次に準備です。ペンの準備、変数の準備、開始点の計算、開始点への移動を行なっています。



式はこうなっています。Rは「定円半径」、rは「動円半径」、dは「描画点半径」、θは角度です。
\[ x=(R-r)\cos(\theta)+d\cos\left(\frac{R-r}{r}\theta\right) \\
y=(R-r)\sin(\theta)-d\sin\left(\frac{R-r}{r}\theta\right) \] この式をプログラムにすると次のようになります。



移動はいつも通りです。



完成版はこちら。

タグ：SCRATCH 平面曲線 三角関数 内トロコイド

外トロコイド Epitrochoid

Scratchで外トロコイドを描きます。式は前回の内サイクロイドや前々回の外サイクロイド、以前のスピログラフに似ています。



曲線を描く処理の詳細は初回で説明していますので、そちらを参照してみてください。違う曲線ですが流れは同じです。

最初に変数です。上のWikipediaのリンクを見るとわかりますが、外トロコイドは中心の定円のまわりを動円が回転する軌跡になっています。このため、内側の円の「定円半径」と回転する円の「動円半径」、さらに動く円の中心から描画点までの「描画点半径」を変数として持っています。これら三種類の半径はスライダー表示にして画面上で値を変更できるようにしています。値を変えると曲線の形が変わります。



次に本体です。角度を0.5度ずつ変化させながら描画を続けます。繰り返しの終了条件がないのは、スライダーで指定する各半径の値によって終了条件が変わるからです。描画を止めるには、旗の右にある赤いボタンを押してください。描画には時間がかかるのでターボモードがお勧めです。



次に準備です。ペンの準備、変数の準備、開始点の計算、開始点への移動を行なっています。



式はこうなっています。Rは「定円半径」、rは「動円半径」、dは「描画点半径」、θは角度です。
\[ x=(R+r)\cos(\theta)-d\cos\left(\frac{R+r}{r}\theta\right) \\
y=(R+r)\sin(\theta)-d\sin\left(\frac{R+r}{r}\theta\right) \] この式をプログラムにすると次のようになります。



移動はいつも通りです。



完成版はこちら。

タグ：平面曲線 三角関数 SCRATCH 外トロコイド